Механика (современная физика)

ГЛАВА1

КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ И

ПРОСТЕЙШИХ СИСТЕМ

 

1.1. Теоретический материал

Физическая величина – это количественная характеристика свойства материальных объектов или явлений (процессов). Каждая физическая величина устанавливается однозначным способом ее измерения – экспериментального определения или расчета. Определение физической величины указывает принципиальный способ ее измерения.

Физическое понятие (модель объекта или явления) – это абстракция (филос.), которая отражает только основные, наиболее существенные, свойства материальных объектов или явлений (процессов).

Критерий правильности выбора модели. Если в данной задаче физическая величина, описывающая неосновное свойство, от которого мы абстрагируемся, много меньше другой, характерной для этой задачи, величины той же размерности, то модель выбрана верно.

Заметим, что один и тот же материальный объект или одно и то же явление в различных условиях могут быть рассмотрены в рамках различных моделей, если они удовлетворяют критериям правильности выбора этих моделей.

Тело отсчета – тело, относительно которого рассматривается движение других тел.

Часы – неподвижный относительно тела отсчета прибор для измерения времени, принцип действия которого основан на сравнении длительности исследуемого временного интервала с длительностью выбранного за эталон периодического процесса.

Система отсчета – совокупность системы координат^[1], связанной с телом отсчета, и набора синхронизированных часов, размещенных в разных точках координатной системы.

Условие синхронизации часов A и B, расположенных в разных точках системы отсчета (в предположении об изотропности пространства):

                                                                           (1.1)

Здесь  – момент времени излучения из точки A светового сигнала (кванта света) по часам в точке A,  – момент времени регистрации этого сигнала в точке B по часам в точке B,  – момент времени регистрации в точке A отраженного в точке B сигнала по часам в точке A.

Материальная точка – физическое понятие (модель, абстракция), представляющее тело, размерами (и формой) которого можно пренебречь в условиях данной задачи.

Положение материальной точки относительно данной системы отсчета (в данной системе отсчета) S задается ее координатами или радиус-вектором .

Радиус-вектор материальной точки  относительно данной системы отсчета – вектор, начало которого находится в начале координат этой системы, а конец – в месте расположения материальной точки (см. рис. 1.1а):

,                                                      (1.2)

где ,  и  – орты декартовой системы координат: , , ; x, y, z – координаты материальной точки.

 

 

 

 

 

 

 

 

 

 

 

 

 

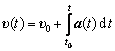Закон движения материальной точки относительно данной системы отсчета – зависимость радиус-вектора или координат материальной точки от времени:

                                                                                 (1.3)

Траектория движения материальной точки – линия, описываемая в пространстве концом радиус-вектора материальной точки.

Уравнение траектории задается совокупностью двух уравнений

                                                                        (1.4)

которые можно получить, исключая время из закона движения в координатной форме (1.3). Заметим, что сам закон движения в координатной форме представляет собой уравнение траектории, заданное в параметрическом виде.

Перемещение материальной точки  – изменение радиус-вектора материальной точки за время Dtс момента времени t (рис. 1а):

.        (1.5)

Скорость материальной точки  относительно данной системы отсчета – физическая величина, равная производной радиус-вектора материальной точки по времени (производная берется при постоянных ортах системы координат, поскольку они жестко связаны с телом отсчета):

,                                                              (1.6)

где , ,  – проекции скорости  на соответствующие оси системы координат. Скорость  можно представить в виде суммы составляющих скорости вдоль осей системы координат:

.            (1.7)

При этом модуль скорости  равен

.                                                              (1.8)

В соответствии с определением скорость всегда направлена по касательной к траектории (см. рис. 1.1б).

Зная закон изменения скорости материальной точки , и радиус-вектор  в начальный момент времени t₀, можно найти закон движения:

.                                                                 (1.9)

Путь s(t), пройденный материальной точкой вдоль траектории (длина траектории) за время t, равен

,                                                                       (1.10)

при этом модуль скорости  в любой момент времени равен

.                                                    (1.11)

Ускорение материальной точки  относительно данной системы отсчета – физическая величина, равная производной скорости материальной точки по времени (при постоянных ортах системы координат):

,           (1.12)

где a_x, a_y, a_z – проекции ускорения  на соответствующие оси системы координат. Ускорение  можно представить в виде суммы составляющих ускорения вдоль осей системы координат:

.       (1.13)

При этом модуль ускорения  равен

.                                                             (1.14)

Зная закон изменения ускорения материальной точки , а также скорость  и радиус-вектор  в начальный момент времени t₀, можно найти закон изменения скорости и закон движения:

,                                                                (1.15)

.                                (1.16)

Начальные условия для материальной точки – значения радиус-вектора и скорости в начальный момент времени t₀ относительно заданной системы отсчета:

                                                                             (1.17)

Тангенциальное ускорение  – составляющая ускорения  вдоль направления скорости  (см. рис. 1.2):

, , ,                      (1.18)

,                                                             (1.19)

где  – проекция ускорения  на направление скорости .

 

 

 

 

 

 

 

 

 

 

Движение материальной точки при  – ускоренное, при  – замедленное, при  – равномерное, а при  – равнопеременное.

Нормальное ускорение  – составляющая ускорения , перпендикулярная направлению скорости (рис. 1.2):

, , ,                               (1.20)

где  – проекция ускорения  на направление , перпендикулярное скорости и направленное к центру кривизны траектории.

Нормальное ускорение всегда направлено к центру кривизны траектории – центру окружности максимального радиуса (радиуса кривизны траектории), касательной к траектории в данной точке, при этом

,                                                                   (1.21)

где  – радиус кривизны траектории в данной точке, а  – угол между скоростями в моменты времени t и t + dt.

Ускорение  можно представить в виде суммы нормального  и тангенциального  ускорений:

.                                                                 (1.22)

При этом модуль ускорения  равен

.                                                            (1.23)

В соответствии с (1.21) и (1.22) ускорение всегда отклонено от направления скорости в сторону центра кривизны траектории в данной точке, то есть внутрь траектории (см. рис. 1.2).

В частном случае движения материальной точки по окружности, т.е. движения в плоскости по траектории с постоянным радиусом кривизны –  (рис. 1.3), можно ввести угловую скорость  иугловое ускорение :

  (1.24)

При этом:

                                                           (1.25)

Механическая система – совокупность материальных тел.

Система материальных точек – совокупность тел, каждое из которых можно считать материальной точкой. Далее будем считать, что всякую рассматриваемую нами механическую систему можно рассматривать как систему материальных точек.

Абсолютно твердое тело – тело (система материальных точек), расстояния между двумя любыми материальными точками которого не меняются в условиях данной задачи.

Поступательное движение абсолютно твердого тела – движение, при котором прямая, соединяющая любые две материальные точки тела, перемещается параллельно самой себе.

Принцип суперпозиции движений – в случае поступательного движения системы отсчета S¢ относительно системы S (рис. 1.4) радиус-вектор (скорость, ускорение) произвольной материальной точки относительно системы S равен сумме радиус-векторов (скоростей, ускорений) начала отсчета O' системы S' и той же материальной точки относительно системы S':

                                                                (1.26)

Здесь  и  – переносные скорость и ускорение соответственно.

 

 

 

 

 

 

 

 

 

 

 

 

Уравнения кинематической связи – уравнения, связывающие кинематические характеристики различных тел системы:

                                                               (1.27)

Существуют два способа нахождения уравнений кинематической связи.

Способ 1. Принцип независимых перемещений. Перемещение какого-либо тела в системе связанных тел складывается из так называемых «независимых» перемещений, каждое из которых обусловлено (вызвано) перемещением соответствующего другого тела системы при покоящихся остальных телах:

.                                                                          (1.28)

Способ 2. Записать величины постоянных кинематических характеристик элементов связей (нитей, штанг, блоков, поверхностей и т.д.) через координаты тел системы, используя свойства этих элементов (нерастяжимость, неподвижность, недеформированность), и продифференцировать эти величины по времени.

 

1.2. Основные типы задач и методы их решения

 

1.2.1. Классификация задач кинематики

Основной задачей кинематики является определение кинематических характеристик тел, движущихся относительно данной системы отсчета.

Большинство задач кинематики можно условно отнести к следующим типам задач или их комбинациям:

1) кинематика материальной точки,

2) принцип суперпозиции движений,

3) уравнения кинематической связи,

4) кинематика простейших механических систем.

Как правило, один из типов задач имеет основное, другие – подчиненное по отношению к условию задачи значение.

 

1.2.2. Общая схема решения задач кинематики

I. Определиться с моделями материальных объектов и явлений.

1. Нарисовать чертеж, на котором изобразить рассматриваемые тела.

2. Выбрать систему отсчета и изобразить на чертеже ее систему координат (из соображений удобства).

3. Изобразить и обозначить кинематические характеристики тел.

4. Выбрать модели тел и их движения (если это не сделано в условии задачи).

II. Записать полную систему уравнений для искомых величин.

1. Записать в проекциях на оси координат:

а) законы движения,

б) законы изменения скорости,

в) законы изменения ускорения.

2. Записать начальные условия.

3. Записать уравнения кинематических связей.

4. Использовать результаты ранее решенных задач и особые условия задачи (например, заданные соотношения между характеристиками системы).

III. Получить искомый результат в аналитическом и численном видах.

1. Решить систему полученных уравнений.

2. Провести анализ решения (проверить размерность и лишние корни, рассмотреть характерные случаи, установить область применимости).

3. Получить численный результат.

 

Примечания.

В случае решения задач на кинематику материальной точки в пп. I.3 – II.2 речь идет о кинематических характеристиках материальной точки, а п. II.3 надо опустить.

В случае решения задач на кинематику простейших механических систем в пп. I.3 – II.2 речь идет о кинематических характеристиках тел рассматриваемой системы.

Пункты II.1 – II.3 (в том числе II.2.a – II.2.в) можно выполнять в той или иной последовательности в зависимости от типа задачи.