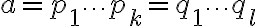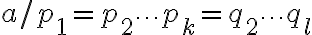Введение в теорию делимости

Теорема. Каждое натуральное большее единицы число представляется в виде произведения простых чисел, причём единственным образом (с точностью до перемены множителей местами).

Доказательство. Уже было доказано, что каждое такое число можно хотя бы каким-нибудь образом представить в виде произведения простых. Докажем методом математической индукции по величине рассматриваемого числа, что его представление в виде произведения простых единственно. Наименьшее из натуральных чисел, превышающих единицу, это число 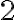$2$. Оно является простым и поэтому допускает единственное разложение на простые (произведение из одного сомножителя - самого себя). Пусть число 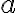$a$ больше двух и допускает два различных разложения на простые:

$a=p_1\cdots p_k=q_1\cdots q_l$.

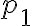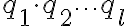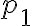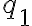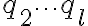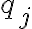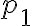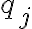Простое число $p_1$ делит произведение $q_1\cdot q_2\cdots q_l$. По доказанной в задании лемме, если $p_1$ не делит $q_1$, то тогда оно делит $q_2\cdots q_l$. Продолжая это рассуждение мы рано или поздно найдём такое $q_j$, которое делится на $p_1$. Но $q_j$ - простое число, поэтому его делитель 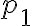$p_1$ равен ему самому: 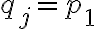$q_j=p_1$. Для простоты обозначений будем считать, что 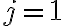$j=1$. Разделим наше равенство на число 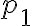$p_1$ (оно же 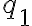$q_1$). Получим

$a/p_1=p_2\cdots p_k=q_2\cdots q_l$.

C одной стороны, мы имели два различных разложения, а сократили на одно и то же число. Значит после сокращения снова получится два различных разложения. С другой стороны, число 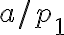$a/p_1$ меньше, чем 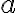$a$, и по предположению индукции оно раскладывается на простые единственным образом. Полученное противоречие означает, что наше предположение о наличии у числа 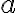$a$ двух различных разложений на простые было неверным. Это завершает доказательство теоремы.