Попеленский М.Ю.
Стационарные движения динамических систем. Линеаризация
Теория
Управляемые динамические системы (УДС), как правило, описываются при помощи систем нелинейных дифференциальных уравнений вида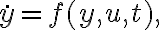
где 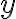 --- вектор состояния размерности
--- вектор состояния размерности 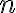 ,
, 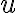 -- вектор управления размерности
-- вектор управления размерности  ,
, 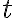 --- время,
--- время,  --- вектор-функция, принадлежащая определенному классу. В дальнейшем, если не оговорено иного, функцию
--- вектор-функция, принадлежащая определенному классу. В дальнейшем, если не оговорено иного, функцию  будем считать дифференцируемой функцией своих аргументов. Если правые части системы явным образом не зависят от времени, она называется автономной, в противном случае --- НЕ автономной. В случае, когда управление выбрано, как функция времени и (или) фазовых координат, анализ движения УДС может производиться методами анализа систем дифференциальных уравнений.
будем считать дифференцируемой функцией своих аргументов. Если правые части системы явным образом не зависят от времени, она называется автономной, в противном случае --- НЕ автономной. В случае, когда управление выбрано, как функция времени и (или) фазовых координат, анализ движения УДС может производиться методами анализа систем дифференциальных уравнений.
Предположим, что исходя из некоторых соображений, например, простоты реализации или минимизации какой-то целевой функции, выбрано управление 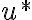 , которое в дальнейшем будем называть желаемым, или программным управлением, а соответствующее ему движение УДС --- желаемым, или программным, движением. В этом случае естественна постановка задачи анализа устойчивости желаемого движения. На первом этапе эта задача традиционно сводится к анализу устойчивости тривиального решения уравнения в отклонениях.
, которое в дальнейшем будем называть желаемым, или программным управлением, а соответствующее ему движение УДС --- желаемым, или программным, движением. В этом случае естественна постановка задачи анализа устойчивости желаемого движения. На первом этапе эта задача традиционно сводится к анализу устойчивости тривиального решения уравнения в отклонениях.
Рассмотрим разность между желаемым движением и реальным, сохранив индекс 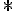 для переменных, отвечающих желаемому движению:
для переменных, отвечающих желаемому движению: 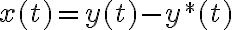 , где через
, где через 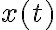 обозначено отклонение от желаемого движения. Отклонение управлений от желаемых обозначим через
обозначено отклонение от желаемого движения. Отклонение управлений от желаемых обозначим через 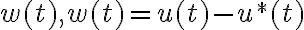 . Запишем дифференциальное уравнение в отклонениях:
. Запишем дифференциальное уравнение в отклонениях: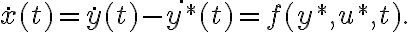
Полагая отклонения управлений и фазовых траекторий малыми, разложим правую часть уравнения в ряд Тейлора, и, удерживая члена первого порядка малости, получим уравнение в отклонениях в виде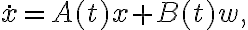
где 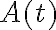 и
и 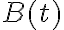 матрицы размерности
матрицы размерности 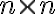 и
и 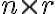 соответственно. В большинстве задач данного сборника матрицы полагаются независимыми от времени.
соответственно. В большинстве задач данного сборника матрицы полагаются независимыми от времени.
В приложениях часто рассматривается задача линейного синтеза, или построения управления  в виде линейной обратной связи по отклонению
в виде линейной обратной связи по отклонению 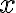 :
: 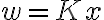 , где
, где 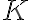 --- матрица, элементы которой подлежат выбору с целью обеспечения устойчивости тривиального решения уравнения в отклонениях.
--- матрица, элементы которой подлежат выбору с целью обеспечения устойчивости тривиального решения уравнения в отклонениях.
Важным частным случаем программного движения является стационарное программное движение, при котором производные от фазовых координат, не являющихся циклическими, равны нулю, а от циклических --- константам.
Напомним определения устойчивости.
Определение 1. Тривиальное решение системы 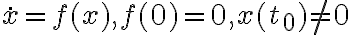 называется устойчивым по Ляпунову, если
называется устойчивым по Ляпунову, если 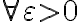
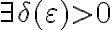 такое, что из выполнения условия
такое, что из выполнения условия 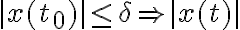
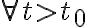 .
.
Определение 2. Тривиальное решение называется асимптотически устойчивым, если оно устойчиво по Ляпунову и существует открытая окрестность нуля 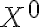 такая, что
такая, что 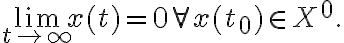
Множество 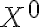 начальных условий, для которых выполнено условие асимптотической устойчивости, называют областью притяжения тривиального решения. Если это множество совпадает с пространством состояний, то решение
начальных условий, для которых выполнено условие асимптотической устойчивости, называют областью притяжения тривиального решения. Если это множество совпадает с пространством состояний, то решение 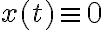 называют асимптотически устойчивым в целом, или глобально асимптотически устойчивым.
называют асимптотически устойчивым в целом, или глобально асимптотически устойчивым.
Для систем уравнений в отклонениях вида 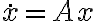 , справедливо следующее утверждение:
, справедливо следующее утверждение:
Теорема. Тривиальное решение системы асимптотически устойчиво тогда и только тогда, когда все собственные числа 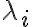 матрицы
матрицы 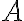 имеют отрицательные действительные части.
имеют отрицательные действительные части.
Действительные части всех корней уравнения
с действительными коэффициентами будут отрицательны, если выполнен критерий Рауса -- Гурвица.

社交网络