Введение в теорию делимости

Все натуральные числа, большие единицы, подразделяются на простые и составные. Простые числа имеют ровно два различных делителя - это единица и само число. Составные числа имеют более двух различных делителей, в том числе они обязательно делятся на число превышающее единицу, но меньшее самого рассматриваемого числа.

Любое превышающее единицу натуральное число имеет хотя бы один простой делитель. Например, наименьший (из превышающих единицу) делитель заданного числа обязательно будет простым, поскольку составное число всегда имеет делитель ещё меньше себя самого.

Теорема. Простых чисел бесконечно много.

Приведём доказательство Евклида. Пусть, от противного, простых чисел лишь конечное число, а именно 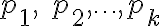$p_1,\ p_2,\ldots ,p_k$. Тогда рассмотрим число 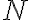$N$, которое на единицу больше, чем произведение всех простых чисел: 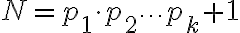$N=p_1\cdot p_2\cdots p_k+1$. С одной стороны у числа 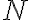$N$ обязан быть хотя бы один простой делитель. С другой стороны при делении числа 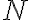$N$ на любое простое число остаётся 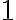$1$ в остатке. Полученное противоречие означает, что наше предположение о конечности числа простых чисел было неверным, что и завершает доказательство теоремы.

Заметим, что превышающие единицу натуральные числа не только имеют простой делитель, но могут даже быть представлены в виде произведения нескольких (возможно только одного) сомножителей, каждый из которых являлся бы простым, или, как это иначе называют, могут быть разложены на простые числа. Действительно, простые числа сами по себе являются таким произведением, состоящим из одного сомножителя. Для составных же чисел это утверждение можно доказать методом математической индукции по величине рассматриваемого числа. Наименьшим составным числом является 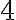$4$. Это число является произведением двух простых чисел, каждое из которых равно 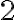$2$. Пусть теперь имеется произвольное составное число 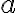$a$, большее четырёх. У него есть хотя бы один простой делитель. Обозначим его 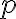$p$. 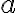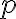Частное от деления $a$ на $p$ обозначим 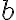$b$, так что 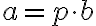$a=p\cdot b$. При этом либо 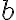$b$ простое и тогда 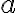$a$ уже представлено в виде произведения двух простых чисел, либо 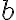$b$ составное, но меньшее по величине, чем 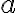$a$. Тогда по предположению индукции 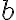$b$ раскладывается на простые множители. Скажем, 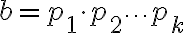$b=p_1\cdot p_2\cdots p_k$. 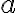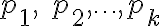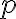Получаем, что $a$ равно произведению сомножителей $p_1,\ p_2,\ldots ,p_k$ и $p$, что и завершает доказательство утверждения.